|
Subwoofer design1 - Box construction 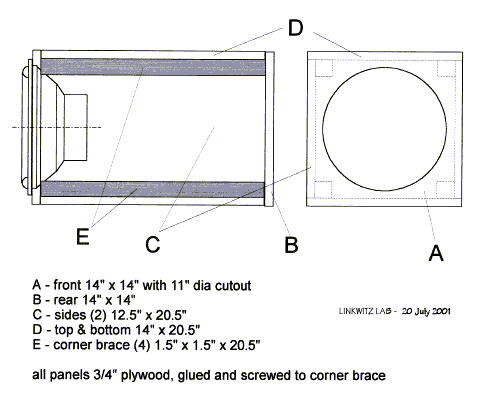
All joints are glued and strengthened with sheetrock
screws. The driver is screwed to the front panel with a rubber gasket (neoprene
weather stripping tape) under its flange. The box is completely sealed except
for a small pin hole (<1 mm diameter) to equalize internal with external static
pressure and to prevent displacing the cone from its normal resting position. No
stuffing is used, to avoid nonlinear friction losses in case the material moves
with cone displacement. The reduction in box resonance frequency that the
stuffing could provide is not important, when the cut-off response is
electronically controlled. The first internal air cavity resonance occurs when the
20.5" length equals 1/2 wavelength. This is at 330 Hz and far outside the
frequency range of interest. The internal volume of the box is about 47 liter.
The sound pressure level inside the
box can get extremely high, but the additional distortion
due to the non-linear force of the inside air upon the cone is small
compared to distortion of the driver motor. 2 - Driver and box model The electrical model uses the force --> current (velocity --> voltage) analogy between mechanical and electrical impedances. The conversion from acoustical impedances (p/q) to mechanical impedances (F/v), which involves Sd, and the conversion from mechanical to electrical impedances (V/I), with the use of Bl, is described in books on electro-acoustics. The electrical impedance model looks like the following circuit with component values derived from the XLS 830500 driver specifications and a 47 liter box. See closed-box1.xls for calculation of the values.
The circuit can be simplified by combining the two
parallel inductors that represent driver and box compliance, and by combining
the resistors for the viscous losses in driver and box. The reactance due to Le
can be neglected at low frequencies compared to Re. Also, the power amplifier
output resistance and speaker cable resistance Rs is
insignificant when compared to Re. The reactive component Mma of the
complex acoustic radiation impedance is very small compared to the moving mass Mms of the driver.
Also, the
corresponding capacitive reactance is much larger than the radiation resistance
Ra. Thus, both will be ignored. It is worth noting that the electrical power
dissipated in Ra is the same as the acoustic power radiated for a given
amplifier voltage Vs. From the radiated power it is easy to determine the sound
pressure at some distance in free-space, via sound intensity and free-space
impedance. The sound pressure can also be derived from the cone velocity v, which is proportional to the voltage V2.
The circuit behavior is most conveniently analyzed with a program like CircuitMaker
.
The derivation of formulas (1) and (2) from the circuit diagram takes a little effort using complex number algebra. At resonance, f = f0, the circuit simplifies to two resistors, Re and R, which allows to determine the relationship between voltage V2 and velocity v. All these quantities are calculated in a spreadsheet. The derivations above are mainly given for a better understanding of the inner workings of the spreadsheet and of the use and limits for the model. 3 - Spreadsheet results Install the Excel 97/2000 Viewer on your computer, if you do not have access to the Microsoft Excel spreadsheet program. [Spec's] - Block 1 has the specifications
of the XLS 830500. You can enter different driver parameters, but only change the
bold faced numbers. Changing any other numbers will erase the underlying
formulas. Note that if you enter VAS it will calculate Cms, in case this
specification is not available. The results of the calculations are best observed in graphical format. [Vp & Ip] - The curves show the required peak current and peak voltage from the power amplifier to obtain Xmax at different frequencies. The current has a minimum at the driver resonance. At low frequencies the amplifier is likely to run into current clipping before Xmax is reached. Reduce Vb to 23 liter, such as when a second driver is added at the other end of the box above, and you see how the current of each driver increases to unrealistic values. At frequencies above resonance the amplifier is likely to clip at its supply voltage. If the driver had a less strong motor with Bl = 10 N/A, then again the current demand on the amplifier would limit the maximum obtainable cone excursion. [Power & SPL] - The SPL at 1 m increases at 12 dB/oct rate for constant excursion Xmax. Free-space is assumed. See Estimates for SPL in a room. Three power curves are shown. The middle one is the product of rms current and rms voltage in VA. The other two power curves show the 8 ohm power rating that an amplifier would have to have, in order to deliver the required peak current or peak voltage, that are necessary to reach Xmax. It is clear that Xmax is difficult to reach above the resonance frequency with typical amplifiers. Since the SPl is already high at these frequencies there is no need for such large excursions. [SPL @ 2.83 V] - The graph shows the SPL frequency response of the driver mounted in the box for a constant drive voltage of 2.83 V, which would correspond to 1 W into 8 ohm. The actual amplifier load impedance differs completely from 8 ohm, but that is no problem for any well designed solid-state amplifier. The only limits are the amplifier's output current capability and maximum output voltage swing. The response shows a broad roll-off, as would be expected from the low Qt = 0.4. The woofer obviously needs equalization to be useful. If you enter Bl = 10 N/A for the driver, then the response shows the more typical highpass behavior, but the voltage sensitivity is reduced since the motor has less strength. [SPL & Ip @ 10Vp] - Knowing a power amplifier's
maximum output current and voltage swing this graph allows to estimate the
maximum SPL that can be obtained when using it. The SPL can, of course, not
exceed the excursion limited SPL from the [Vp & Ip] tab. [Max SPL @ Vpeak] -
The power amplifier to be used can be specified in Block
7 and the available peak voltage is calculated. For this peak voltage the
maximally obtainable SPL is plotted. Typically, at low frequencies the SPL is
excursion limited and Vpeak exceeds what is necessary. At higher frequencies the
SPL becomes voltage limited, provided that the amplifier is capable of
delivering the necessary peak current. [Impedance] - The impedance of the driver by itself and in the box. When the calculated box impedance is compared to an actual measurement, one can get an idea of the box losses and of Qb. The remaining two tabs, [Test] and [EQ], are discussed on the following pages.
|