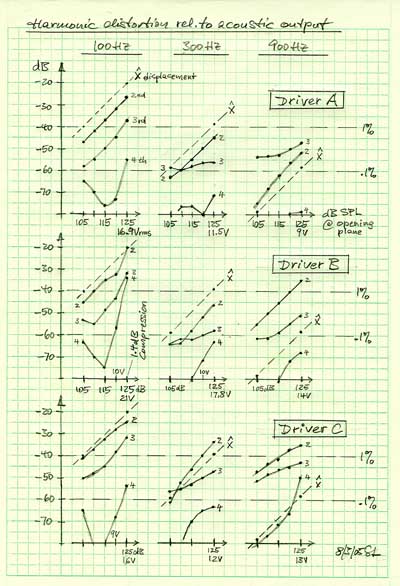| Page 1 | Page 2 | Page 3 | Page 4 | Page 5 |

Issues in loudspeaker design - 3

O - Unreasonably high distortion in midrange drivers?

P - Estimate of L_e(x) induced distortion at high frequencies

Q - Estimate of L_e(i) induced distortion at high frequencies

R - Recommended study material about distortion in loudspeaker drivers

---------------------------------------------------------------------------

O - Unreasonably high distortion in midrange drivers?

The nonlinear relationship between SPL, excitation frequency and harmonic distortion products was investigated for three small midrange drivers as part of a search for an eventual replacement of the Peerless HDS 134, 850488, 5.25" driver that is used for PLUTO. Typically distortion increases with SPL or cone displacement. For constant SPL the displacement decreases as 1/f² with increasing frequency and it could be expected that distortion decreases correspondingly.

In a linear system the output 'y' is proportional to the input 'x' as in
y = a₁ x
In a nonlinear system the relationship between input and output is often of the form
y = a₀ + a₁ x + a₂ x² + a₃ x³ + .....+ a_n xⁿ    which is a power series expanded around x = 0.
If the input is a sinusoidal voltage 
x = A sin(wt), then
x² = A² [1 - 0.5 cos(2wt)]  
x³ = A³ [0.75 sin(wt) - 0.25 sin(3wt)]
x⁴ = A⁴ [0.375 - 0.5 cos(2wt) + 0.125 cos(4wt)] 
and so on for higher powers of x. Thus harmonics nw are generated and dc terms.w will also decrease by dA (-1 dB), but the second harmonic amplitude will decrease by dA² (-2 dB), the third harmonic amplitude by dA³ (-3 dB), the fourth by dA⁴ (-4 dB), and so on, at least to a first order approximation.

The sound output from the unbaffled driver was measured with the microphone in the center of the plane that touches the driver's roll surround. Drive voltages are listed for 125 dB SPL. The amplitude of the harmonics is plotted relative to the fundamental. The fundamental amplitude was changed in 5 dB increments from 105 dB to 125 dB SPL. The dashed lines x show the relative change in cone excursion with SPL and frequency. Driver A is the Peerless 850488, the other two drivers were samples under consideration.

Driver A 100 Hz - The relative amplitude change of the 2nd harmonic behaves exactly as expected. The 3rd harmonic starts out with the right slope for high SPL but then decreases more slowly. The 4th behaves strange at low levels. 300 Hz - Excursion x has decreased by 19 dB. The 2nd harmonic follows but not the others. 900 Hz - Excursion x has decreased by 38 dB. The distortion products do not drop correspondingly. Driver B 100 Hz - Slightly higher distortion than driver A. Serious misbehavior above 120 dB SPL. 300 Hz - Slightly lower distortion than driver A and similar behavior. 900 Hz - Large amount of 2nd harmonic. Again all distortion products are much higher than expected from the reduction in excursion. Driver C 100 Hz - Worse than drivers A and B.  300 Hz - The 2nd and 3rd harmonics have dropped less than in the other drivers. 900 Hz - High levels of distortion.

The dominant nonlinear parameters in a driver are the force factor Bl(x), the stiffness of suspension K_ms(x), and the electrical inductance L_e(x). The effect of Bl(x) and K_ms(x) should decrease as 1/w² with frequency, but since the inductance increases as wL_e its effect should only decrease as 1/w and possibly overtake the effects of the other two non-linearities. At least that is what has been suggested to me. All these parameters can be measured with a Klippel Analyzer, at least for low frequencies. In the following I will estimate the L_e(x) induced distortion based on measured L_e(x) for drivers A and B.
Top

P - Estimate of L_e(x) induced distortion at high frequencies

The voice coil inductance changes with displacement x in a nonlinear fashion as seen is the graphs for Driver A and Driver B. The behavior for small excursions around  x = 0  can be approximated by the two expressions for L_e below.  

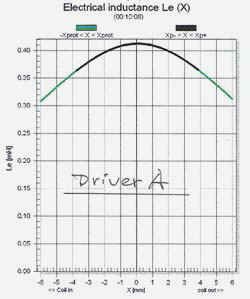
LeA = 410 mH - 70 mH (x / 5 mm)2

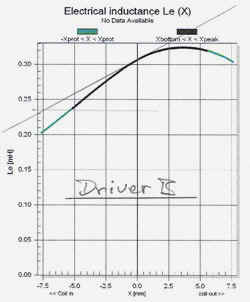
LeB = 305 mH + (70 mH / 7.5 mm) x

In general, L_e(x) can be expanded as   L_e(x) = L₀ + L₁ x + L₂ x² + ....  [1]  
where  L_0A = 410 mH,   L_1A = 0,   L_2A = 2.8 mH/mm² 
and  L_0B = 305 mH,   L_1B = 9.33 mH/mm  

1 - Electrical impedance change due to L_e(x)

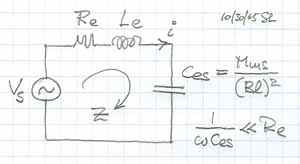
With a current i flowing through the coil the reactive voltage across the inductance L_e(x) becomes both a function of i and of resulting displacement x

v_Le = L_e di/dt + i (dL_e/dx) (dx/dt)    [2]

The displacement x follows from the relationship between applied force F = Bli and cone acceleration a in the mass controlled region of driver operation far above f_s

F = Bli = M_ms a    [3]

For sinusoidal displacement  x = X sin(wt)   
the velocity is   dx/dt = w cos(wt) = w x    [4]       
and the acceleration is   a = d²x/dt² = -w² x     
thus  Bli = M_ms w² x   
and   x = Bli / (w² M_ms) = K i    [5]    
where   K = Bl / (w² M_ms)

The current is  i = v1 / Z    [6] and for sinusoidal voltage   v1 = Vs sin(wt)   the current becomes   i = (Vs/Z) sin(wt)  and thus di/dt = w (Vs/Z) cos(wt) = w i    [7] Z = sqrt [ (Re)2 + (wL0)2 ]    [8]

Finally from differentiating [1] above  dL_e/dx = L₁ + 2 L₂ x    [9]

Inserting [4, 5, 7, 9] into [2] yields the voltage across the inductance   

v_Le = i wL₀ + i² K wL₁ + i³ 2 K² wL₂    [10]

Where
i = v₁ / Z = (V_s/Z) sin(wt)
i² = (V_s/Z)² [1 - 0.5 cos(2wt)]  
i³ = (V_s/Z)³ [0.75 sin(wt) - 0.25 sin(3wt)]

So approximately   v_Le = i wL₀ - 0.5 (V_s/Z)² K wL₁ cos(2wt) - 0.5 (V_s/Z)³ K² wL₂ sin(3wt)

With a 2nd harmonic generator   v2 = 0.5 (Vs/Z)2 K wL1     and a 3rd harmonic generator    v3 = 0.5 (Vs/Z)3 K2 wL2    the relative distortion  becomes  d2 = v2/Vs = 0.5 (wL1/Z) (K Vs/Z)     [11]   and    d3 = v3/Vs = 0.5 (wL2/Z) (K Vs/Z)2   [12]

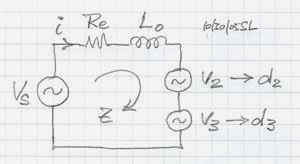Expressed in dB the distortion is   D₂ = 20 log(d₂)   and   D₃ = 20 log(d₃)   

Numerical example 1 for f = 900 Hz

Clearly there is a huge difference between the distortion estimates and the measured values. The questions is why? The mechanical displacements are extremely small and in the order of 30 micron. The displacements that produce the measured distortion are  less than 1 mm. Which nonlinear mechanism is causing the distortion? The currents, magnetic fields, forces and accelerations are the same as at low frequencies for constant SPL, only the excursions are drastically reduced. 

2 - Force generated due to Le(x)

There is a second effect due to L_e(x) that must be considered which is the reluctance force F_L. This force has its useful application in electro-magnetic transducers like door bells and early headphones. Here it is an undesirable remnant. Its magnitude is derived from the energy that is stored in the magnetic field of the voice coil.

W = 0.5 i² L_e(x)
dW/dx = F_L = 0.5 i² dL_e(x) / dx

This force will generate 2nd harmonic distortion with an amplitude d₂ relative to F = Bli 

d₂ = F_L / F = 0.5 i [dL_e(x) / dx] / (Bl)    [13]

Numerical example 2 for f = 900 Hz

For Driver A the gradient of L_e(x) is zero and thus this type of distortion is zero. For Driver B the calculated distortion is still by an order of magnitude lower than the measured value. Thus I draw the conclusion that in these two cases the reluctance force is not the dominant factor. 

Estimates 1 and 2 do not mean, though, that L_e(x) is insignificant for distortion at high frequencies. They only mean that for a high frequency excitation signal, with its very small voice coil displacement x, there is no significant amount of harmonic distortion generated. But, if a low frequency signal is present together with the high frequency signal, then the large low frequency voice coil displacements can cause large amounts of intermodulation distortion products near the high frequency signal due to the large low frequency variation of L_e(x). 
Top

Q - Estimate of L_e(i) induced distortion at high frequencies

The voice coil inductance changes also as a function of the current flowing through it. The magnetic field strength H(i) that is generated by the voice coil current produces nonlinear increases and decreases mH(i) of the static magnetic bias flux density B that is generated by the permanent magnet. The permeability m of the magnetic circuit changes nonlinearly and with hysteresis losses. 

The relationship between magnetic flux F and inductance is  F = L_e(i) i   where    F = [ B + mH(i) ] A

A time change in flux generates a voltage   v = - dF / dt = - i (dL_e(i)/di) (di/dt)

Thus the voltage across the voice coil can be described by

v_Le = L_e di/dt - i (dL_e(i)/di) (di/dt)    [14]

where   di/dt = wi   and   i = V_s/Z   and thus

v_Le = wL_e - i² w dL_e(i)/di    which contains a 2nd harmonic distortion generator   (V_s/Z)² w dL_e(i)/di

Similar to the model for [11] above:

d₂ = (V_s/Z²) w dL_e(i)/di    [15]    due to flux modulation

The value of dL_e(i)/di is not known to me for drivers A and B. I have seen data for a driver where the inductance changed in the order of 3% per ampere without shorting rings and 2%/A with shorting rings.
For the calculation below I have used a value of 3%/A.  

Numerical example 3 for f = 900 Hz

It appears that flux modulation is the dominant mechanism for harmonic distortion at high frequencies in these drivers. Driver A actually has shorting rings and L_e(i) could not have changed by more than 0.5%/A in order to match the calculated value with the measurement. That may indicate a really good choice of materials and design. 

In summary, the measured values do not seem unreasonable, but there is certainly room for improvement of drivers B and C.
Top

-----------------------------------------------------------------------

R - Recommended study material about distortion in loudspeaker drivers

1 - Wolfgang Klippel, "Loudspeaker Nonlinearities - Causes, Parameters, Symptoms", 119th AES Convention, New York, October 2005, Preprint 6584

2 - The following two cutouts are from a new and comprehensive poster "Loudspeaker Nonlinearities - Causes, Parameters, Symptoms" by Klippel at CES 2006

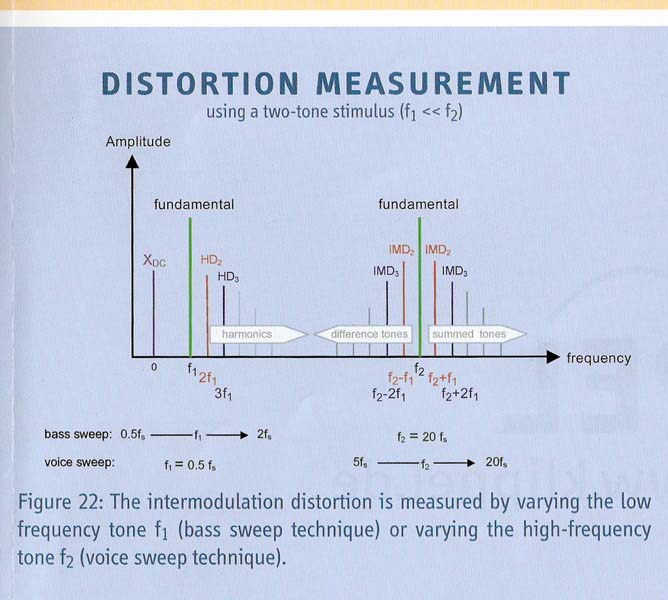
The two stimulus measurement method allows to see and separate out the effects of the dominant driver nonlinearities by measuring distortion in sound pressure, distortion of the voice coil current and dc-displacement.

The table below indicates in which form the symptoms of the nonlinearities show up in the measurements.

3 - "The power of Loudspeaker Models", W. Klippel, Richard Small, David Clark, Jürgen Ringlstetter, Andrew Bright
Panel Workshop, AES SAN FRANCISCO 2004, Transparencies,  PDF

4 - Klippel, "Interactive Listening Test"

5 - Mark Dodd, Wolfgang Klippel, Jack Oclee-Brown, "Voice Coil Impedance as a Function of Frequency and Displacement", 117th AES Convention, San Francisco, October 2004, Preprint 6178
(The effects of impedance variation with current and magnetic hysteresis are not considered in this paper.)

Other nonlinear and linear distortion measurements and procedures can be found on the following pages:

Distortion test of drivers

Woofer measurements

Audibility of allpass crossover phase distortion

Diffraction from baffle edges

-------------------------------------------------------------------

| Page 1 | Page 2 | Page 3 | Page 4 | Page 5 |